نقاط سبز رنگ، نمونه‌هایی از توزیع نرمال دومتغیره‌اند و محور آبی رنگ، مختصات جدید در راستای قرار گرفتن بیشترین تغییرات نمونه بر روی مؤلفه‌های اصلی است.

تحلیل مؤلفه‌های اصلی (Principal Component Analysis - PCA) تبدیلی در فضای برداری است، که بیشتر برای کاهش ابعاد مجموعهٔ داده‌ها مورد استفاده قرار می‌گیرد.

تحلیل مؤلفه‌های اصلی در سال ۱۹۰۱ توسط کارل پیرسون^[۱] ارائه شد. این تحلیل شامل تجزیه مقدارهای ویژهٔ ماتریس کواریانس می‌باشد.

جزئیات[ویرایش]

تحلیل مؤلفه‌های اصلی در تعریف ریاضی^[۲] یک تبدیل خطی متعامد است که داده را به دستگاه مختصات جدید می‌برد به‌طوری‌که بزرگترین واریانس داده بر روی اولین محور مختصات، دومین بزرگترین واریانس بر روی دومین محور مختصات قرار می‌گیرد و همین‌طور برای بقیه.
تحلیل مؤلفه‌های اصلی می‌تواند برای کاهش ابعاد داده مورد استفاده قرار بگیرد، به این ترتیب مؤلفه‌هایی از مجموعه داده را که بیشترین تأثیر در واریانس را دارند حفظ می‌کند.
برای ماتریس داده XTdisplaystyle X^T با میانگین تجربی صفر، که هر سطر یک مجموعه مشاهده و هر ستون داده‌های مربوط به یک شاخصه است، تحلیل مؤلفه‌های اصلی به صورت زیر تعریف می‌شود:

• 
  YT=XTW=VΣdisplaystyle Y^T=X^TW=VSigma
  

به‌طوری‌که VΣWTdisplaystyle VSigma W^T تجزیه مقدارهای منفرد ماتریس XTdisplaystyle X^T می‌باشد.

محدودیت‌های تحلیل مولفه‌های اصلی[ویرایش]

استفاده از تحلیل مؤلفه‌های اصلی منوط به فرض‌هایی است که در نظر گرفته می‌شود. از جمله:

• فرض خطی بودن

فرض بر این است که مجموعه داده ترکیب خطی پایه‌هایی خاص است.

• فرض بر این که میانگین و کواریانس از نظر احتمالاتی قابل اتکا هستند.


• فرض بر این که واریانس شاخصه اصلی داده‌است.

محاسبه مولفه‌های اصلی با استفاده از ماتریس کواریانس[ویرایش]

بر اساس تعریف ارائه شده از تحلیل مؤلفه‌های اصلی، هدف از این تحلیل انتقال مجموعه داده X با ابعاد M به داده Y با ابعاد L است. بنابرین فرض بر این است که ماتریس X از بردارهای X1…XNdisplaystyle X_1dots X_N تشکیل شده‌است که هر کدام به صورت ستونی در ماتریس قرار داده شده‌است. بنابرین با توجه به ابعاد بردارها (M) ماتریس داده‌ها به صورت M×Ndisplaystyle Mtimes N است.

محاسبه میانگین تجربی و نرمال‌سازی داده‌ها[ویرایش]

نتیجه میانگین تجربی، برداری است که به صورت زیر به دست می‌آید:

• u[m]=1N∑i=1NX[m,i]displaystyle u[m]=frac 1Nsum _i=1^NX[m,i]

که به‌طور مشخص میانگین تجربی روی سطرهای ماتریس اعمال شده‌است.

سپس ماتریس فاصله تا میانگین به صورت زیر به دست می‌آید:

• 
  B=X−uhdisplaystyle B=X-uh
  

که h برداری با اندازه 1×Ndisplaystyle 1times N با مقدار ۱ در هرکدام از درایه‌ها است.

محاسبه ماتریس کواریانس[ویرایش]

ماتریس کواریانس C با ابعاد M×Mdisplaystyle Mtimes M به صورت زیر به دست می‌آید:

• C=E[B⊗B]=E[B⋅B∗]=1NB⋅B∗displaystyle C=mathbb E [Botimes B]=mathbb E [Bcdot B^ast ]=frac 1NBcdot B^ast

  
  

  به‌طوری که:

  
  

  
  Edisplaystyle mathbb E میانگین حسابی است.

  
  

  
  ⊗displaystyle otimes ضرب خارجی است.

  
  

  
  B∗displaystyle B^ast ماتریس ترانهاده مزدوج ماتریس Bdisplaystyle B است.

  
  

محاسبه مقادیر ویژه ماتریس کواریانس و بازچینی بردارهای ویژه[ویرایش]

در این مرحله، مقادیر ویژه و بردارهای ویژه ماتریس کواریانس، Cdisplaystyle C، به دست می‌آید.

• V−1CV=Ddisplaystyle V^-1CV=D

V ماتریس بردارهای ویژه و D ماتریس قطری است که درایه‌های قطر آن مقادیر ویژه هستند.
آنجنان که مشخص است، هر مقدار ویژه متناظر با یک بردار ویژه است. به این معنا که ماتریس V ماتریسی M×Mdisplaystyle Mtimes M است که ستون‌های آن بردارهای ویژه می‌باشند و بردار ویژه Vqdisplaystyle V_q در ستون qام قرار دارد و مقدار ویژه qام یعنی درایهٔ λq=Dq,qdisplaystyle lambda _q=D_q,q متناظر با آن است.
بازچینی بردارهای ویژه بر اساس اندازهٔ مقادیر ویژه متناظر با آن‌ها صورت می‌گیرد. یعنی بر اساس ترتیب کاهشی مقادیر ویژه، بردارهای ویژه بازچینی می‌شوند. یعنی p≤q⇒λp≤λqdisplaystyle pleq qRightarrow lambda _pleq lambda _q

انتخاب زیرمجموعه‌ای از بردارهای ویژه به عنوان پایه[ویرایش]

تحلیل مقادیر ویژه ماتریس کواریانس

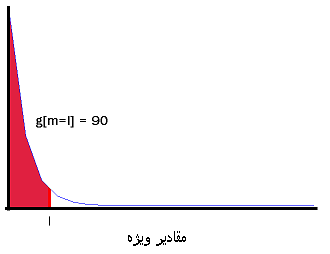
انتخاب زیرمجموعه‌ای از بردارهای ویژه با تحلیل مقادیر ویژه صورت می‌گیرد. زیرمجموعه نهایی با توجه به بازچینی مرحله قبل به صورت V1…Vldisplaystyle V_1dots V_l انتخاب می‌شود. در اینجا می‌توان از انرژی تجمعی استفاده کرد که طبق آن

• g[m]=∑q=1mλqdisplaystyle g[m]=sum _q=1^mlambda _q

انتخاب l باید به صورتی باشد که حداقل مقدار ممکن را داشته باشد و در عین حال g مقدار قابل قبولی داشته باشد. به‌طور مثال می‌توان حداقل l را انتخاب کرد که

• g[m=l]≤90%displaystyle g[m=l]leq 90%

بنابرین خواهیم داشت:

• W[p,q]=V[p,q],p=1…M,q=1…ldisplaystyle W[p,q]=V[p,q],p=1dots M,q=1dots l

انتقال داده به فضای جدید[ویرایش]

برای این کار ابتدا تبدیلات زیر انجام می‌گیرد:
ماتریس sM,1displaystyle s_M,1 انحراف معیار مجموعه داده‌است که می‌تواند به صورت زیر به دست بیاید:

• s[i]=C[i,i]displaystyle s[i]=sqrt C[i,i]

سپس داده به صورت زیر تبدیل می‌شود:

• 
  Z=Bsdisplaystyle Z=frac Bs'

که ماتریسهای Cdisplaystyle C و Bdisplaystyle B در بالا توضیح داده شده‌اند.
داده‌ها می‌توانند به ترتیب زیر به فضای جدید برده شوند:

• Y=W∗.Zdisplaystyle Y=W^ast .Z

نرم‌افزارها[ویرایش]

• در نرم‌افزار متلب تابع princomp مؤلفه‌های اصلی را بازمی‌گرداند که در نسخه‌های جدید، تابع pca جایگزین آن شده‌است.


• Computer Vision Library


• Eviews

جستارهای وابسته[ویرایش]

• تحلیل مولفه‌های مستقل


• تحلیل تفکیک خطی


• تجزیه مقدارهای منفرد


• فشرده‌سازی داده‌ها


• تحلیل تناظر


• فاکتورگیری نامنفی ماتریس

پانویس[ویرایش]

منابع[ویرایش]