برآوردگر کاپلان-مهیر مفاهیم اساسی[ویرایش] منابع[ویرایش] منوی ناوبری2281868Available from UPenn as PDF."Paul Meier, 1924 - 2011"و
میانگینمیانگین حسابیمیانگین هندسیمیانگین همسازمیانهمددامنهانحراف معیارضریب تغییراتصدکدامنه بین چارکیواریانسچولگیکشیدگیگشتاورال-گشتاوردادههای گروهبندیشدهتوزیع فراوانیجدول پیشایندینمودار میلهایدونمودارهنمودار جعبهاینمودار کنترلهمبستگینگارنمودار جنگلیبافتنگارنمودار Q-Qنمودار توالینمودار پراکنشنمودار ساقه و برگنمودار راداریاندازه تأثیرخطای استانداردتوان آماریتعیین اندازه نمونهطراحی آزمایشآزمایش تصادفیانتساب تصادفیتکرار آزمایشبلوکبندیآزمایش عاملیطراحی بهینهتوزیع نمونهگیریآماره بسندهفراتحلیلآماره ترتیبیآماره کاوشیمقدار رکوردکامل بودنخانواده نماییآزمون جایگشتیآزمون تصادفیدنتوزیع نمونهایبوتاسترپینگآماره Uکاراییآمار باثباتاحتمال بیزیاحتمال پیشیناحتمال پسینبازه مورد قبولعامل بیزبرآوردگر بیزیبرآوردگر بیشینهگر احتمال پسینضریب همبستگی پیرسونهمبستگی جزئیاختلاطضریب تشخیصرگرسیون ساده خطی(en)کمینه مربعات خطیمدل خطی عمومی(en)رگرسیون خطی بیزی(en)خانواده نماییرگرسیون لجستیکرگرسیون دوجملهای(en)پواسونکاپای کوهنجدول پیشایندیمدل گرافیرگرسیون پواسونآزمون مکنمارتجزیهتخمین روندفرایند ماناتصحیح فصلیبودنهموارسازی نمایی(en)همجمعیعلیت گرانجرآماره Q(en)آماره دوربین-واتسون(en)خودهمبستگیتابع خودهمبستگی جزئی(en)تابع خودهمبستگی تقاطعی(en)آرمامدل آریماگارچاتورگرسیو برداریتخمین طیفیتحلیل فوریهموجکتابع بقا(en)برآوردگر کاپلان-مهیرآزمون لگرتبهای(en)نرخ خرابیمدل خطرهای متناسب(en)مدل زمان خرابی شتابیده(en)بیوانفورماتیکزیستسنجشیکارآزمایی بالینیمطالعاتهمهگیرشناسیآمار پزشکیآکچوئریسرشماریآمار جرم(en)آمار جمعیتشناسی(en)اقتصادسنجیآمار ملی(en)آمار رسمی(en)جامعه آماریروانسنجی
آنالیز بقابرآوردگربیمسنجیمهندسی قابلیت اطمیناننظریه تخمین
انگلیسیبرآوردگرتابع بقابوم شناسیادوارد ال. کاپلانپل مهیرمجله مؤسسه آماری آمریکاداده سانسورشدهتابع توزیع نمونهایآمار پزشکی
برآوردگر کاپلان-مهیر
پرش به ناوبری
پرش به جستجو
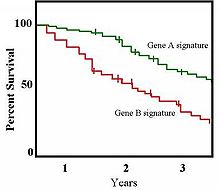
یک مثال از طرح کاپلان–مهیر برای دو وضعیت مرتبط با بقای بیماران
برآوردگر کاپلان–مهیر (به انگلیسی: Kaplan–Meier estimator)،[۱][۲] همچنین معروف به برآوردگر حد محصول، یک برآوردگر برای تخمین تابع بقا از اطلاعات مدت حیات است. در تحقیق پزشکی، اغلب برای اندازهگیری کسر بیماران زنده تا مدت زمانی مشخصی بعد از درمان استفاده میگردد. در اقتصاد، میتوان از آن برای استفاده جهت اندازهگیری مدت زمان افرادی که بعد از از دست دادن شغل بیکار میمانند به کار گرفت. در مهندسی، برای اندازهگیری زمان باقیمانده تا خرابی قطعات یک ماشین مورد استفاده قرار میگیرد. در بوم شناسی، برای برآورد مدت زمان باقی ماندن میوههای گوشتی بر روی گیاهان قبل از اینکه توسط میوه خواران از بین بروند، به کار میرود. برآوردگر بعد از ادوارد ال. کاپلان و پل مهیر نامگذاری شد. هر دوی شان مقالهٔ مشابهی به مجله مؤسسه آماری آمریکا ارسال نمودند، اما ویرایشگر تصمیم گرفت که کار آنها را با ترکیب شان تبدیل به یک مقاله کند، که حدود ۳۴۰۰۰ دفعه از زمان انتشارش مورد ارجاع قرار گرفتهاست.[۳]
مفاهیم اساسی[ویرایش]
طرحی از برآورد تابع بقای کاپلان–مهیر یک سری از مراحل افقی مقدار در حال کاهش است که در آن، وقتی یک نمونه به قدر کافی بزرگ بررسی میشود، تابع بقای صحیح برای آن جمعیت به دست میآید. مقدار تابع بقا بین مشاهدات نمونه برداری شدهٔ موفق متمایز از هم ("تیک ها") ثابت فرض میشود.
مزیت مهم منحنی کاپلان–مهیر این است که این روش بعضی انواع داده سانسورشده را مورد حساب قرار میدهد، بهطور خاص سانسور درست که اگر یک بیمار از مطالعهای به عنوان مثال قبل از مشاهدهٔ نتیجه نهایی، از نمونه خارج شود، رخ میدهد. در طرح، نشانهای تیک کوچک بهطور عمودی نشانگر تلفات هستند، جایی که زمان بقای یک بیمار درست سانسور شده باشد. وقتی هیچ کاهش یا سانسوری رخ ندهد، منحنی کاپلان–مهیر متمم تابع توزیع نمونهای میشود.
در آمار پزشکی، یک کاربرد عادی میتواند بیمارهای گروه بندی شده را در دستههایی قرار دهد، برای مثال، آنهایی که نمایهٔ ژن A را دارند و آنهایی که نمایهٔ ژن B را دارند. در نمودار، بیمارها با ژن B سریع تر از آنهایی که ژن A دارند، میمیرند. بعد از دو سال، حدود ۸۰ درصد بیمارهای با ژن A زنده میمانند، اما کمتر از نصف بیمارهای با ژن B نجات مییابند.
منابع[ویرایش]
↑ Kaplan, E. L.; Meier, P. (1958). "Nonparametric estimation from incomplete observations". J. Amer. Statist. Assn. 53 (282): 457–481. JSTOR 2281868..mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output div[dir=ltr] .cs1-lock-subscription a,.mw-parser-output div[dir=ltr] .cs1-lock-limited a,.mw-parser-output div[dir=ltr] .cs1-lock-registration abackground-position:left .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em
↑ Kaplan, E.L. in a retrospective on the seminal paper in "This week's citation classic". Current Contents 24, 14 (1983). Available from UPenn as PDF.
↑ "Paul Meier, 1924 - 2011". Chicago Tribune. August 18, 2011.
https://en.wikipedia.org/wiki/Kaplan–Meier_estimator ویکیپدیا انگلیسی
ردهها:
- آنالیز بقا
- برآوردگر
- بیمسنجی
- مهندسی قابلیت اطمینان
- نظریه تخمین
(window.RLQ=window.RLQ||[]).push(function()mw.config.set("wgPageParseReport":"limitreport":"cputime":"0.300","walltime":"0.392","ppvisitednodes":"value":2207,"limit":1000000,"ppgeneratednodes":"value":0,"limit":1500000,"postexpandincludesize":"value":322435,"limit":2097152,"templateargumentsize":"value":35510,"limit":2097152,"expansiondepth":"value":16,"limit":40,"expensivefunctioncount":"value":36,"limit":500,"unstrip-depth":"value":1,"limit":20,"unstrip-size":"value":6254,"limit":5000000,"entityaccesscount":"value":1,"limit":400,"timingprofile":["100.00% 288.586 1 -total"," 78.10% 225.373 15 الگو:Navbox"," 40.15% 115.862 1 الگو:پانویس"," 37.82% 109.151 1 الگو:آمار"," 36.20% 104.475 1 الگو:Navbox_with_collapsible_groups"," 34.93% 100.789 1 الگو:Cite_journal"," 18.04% 52.061 1 الگو:انگلیسی"," 16.11% 46.490 1 الگو:به_زبان_دیگر"," 15.22% 43.920 1 الگو:Lang"," 14.07% 40.610 1 الگو:گرداننده_رده"],"scribunto":"limitreport-timeusage":"value":"0.115","limit":"10.000","limitreport-memusage":"value":3327943,"limit":52428800,"cachereport":"origin":"mw1251","timestamp":"20190425232730","ttl":2592000,"transientcontent":false);mw.config.set("wgBackendResponseTime":104,"wgHostname":"mw1261"););